Skip to main content


CALCULUS

SELF-PACED COURSE


1. About this Course

It reviews the fundamentals taught in a one-semester college course in calculus. Our lessons are aligned to the content of the CLEP exam, which covers approximately 60% limits and differential calculus and 40% integral calculus. Algebraic, trigonometric, exponential, logarithmic, and general functions are included.    


"Calculus is synonymous with serious mathematics, and if you watch my course videos, read the supplemental readings, and work hard on the practice problems, you’ll be on your way to being a serious student of mathematics. Calculus as we know it today is much more recent than much of the mathematics you studied: it is only about 350 years old. It forms an illustrious cornerstone in human knowledge, and is the basis for modern physics and economics, among other fields. Working with me, you’ll learn about this incredible subject. Even better, you’ll be learning what you need to pass the CLEP exam in Calculus, to earn college credit. Now more than ever, mathematics is a subject that opens doors-doors to new career opportunities, doors to new intellectual worlds, and doors to new understandings of everyday life. Let’s open them," explains Dr. James Murphy, professor at Johns Hopkins University and instructor of this course.

The Calculus course –completely self-paced and entirely free– is organized into six topical chapters or modules that contain short video lessons, exercises, readings and other interactive resources. 


The goal of the creator of this course –Modern States Education Alliance, a non-profit organization– is to prepare you to pass the College Board's CLEP examination and obtain college credit for free. 


 


2. About the Examination 

It requires to demonstrate an intuitive understanding of calculus and experience with its methods and applications. Knowledge of preparatory mathematics is assumed, including algebra, geometry, trigonometry, and analytic geometry. 

The examination contains 44 questions, in two sections, to be answered in approximately 90 minutes. 

• Section 1: approximately 27 questions, approximately 50 minutes. No calculator is allowed for this section..


• Section 2: approximately 17 questions, approximately 40 minutes. An online graphing calculator (non-CAS) is integrated into the exam software, although only some of the following questions actually require its use: 

• Perform calculations (e.g., exponents, roots, trigonometric values, logarithms)
• Graph functions and analyze the graphs
• Find zeros of functions
• Find points of intersection of graphs of functions
• Find minima/maxima of functions
• Find numerical solutions to equations
• Generate a table of values for a function

To become familiar with the functionality of the calculator prior to taking the exam, download it for free for a 30-day trial period.

3. Required Knowledge and Skills

Questions on the Calculus examination will require you to demonstrate the following abilities:

  • Solving routine problems involving the techniques of calculus (approximately 50% of the exam)

  • Solving nonroutine problems involving an understanding of the concepts and applications of calculus (approximately 50% of the exam)

4. Percentage of Exam Questions

Limits (10%)

  • Continuity

Differential Calculus (50%)

The Derivative

  • Definitions of the derivative


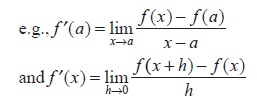
  • Derivatives of elementary functions
  • Derivatives of sums, products and quotients (including tan x and cot x)
  • Derivative of a composite function (chain rule), e.g., sin(ax + b), aekx , ln(kx)
  • Implicit differentiation
  • Derivative of the inverse of a function (including arcsin x and arctan x)
  • Higher order derivatives
  • Corresponding characteristics of graphs of ƒ, ƒ′ and ƒ″
  • Statement of the Mean Value Theorem; applications and graphical illustrations
  • Relation between differentiability and continuity
  • Use of L'Hospital's Rule (quotient and indeterminate forms)

Applications of the Derivative

  • Slope of a curve at a point
  • Tangent lines and linear approximation
  • Curve sketching: increasing and decreasing functions; relative and absolute maximum and minimum points; concavity; points of inflection
  • Extreme value problems
  • Velocity and acceleration of a particle moving along a line
  • Average and instantaneous rates of change
  • Related rates of change

Integral Calculus (40%)

Antiderivatives and Techniques of Integration

  • Concept of antiderivatives
  • Basic integration formulas
  • Integration by substitution (use of identities, change of variable)

Applications of Antiderivatives

  • Distance and velocity from acceleration with initial conditions
  • Solutions of y′ = ky and applications to growth and decay

The Definite Integral

  • Definition of the definite integral as the limit of a sequence of Riemann sums and approximations of the definite integral using areas of rectangles
  • Properties of the definite integral
  • The Fundamental Theorem:


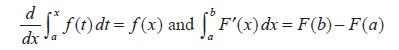
Applications of the Definite Integral

  • Average value of a function on an interval
  • Area, including area between curves
  • Other (e.g., accumulated change from a rate of change)

Notes and Reference Information

  1. Figures that accompany questions are intended to provide information useful in answering the questions. All figures lie in a plane unless otherwise indicated. The figures are drawn as accurately as possible EXCEPT when it is stated in a specific question that the figure is not drawn to scale. Straight lines and smooth curves may appear slightly jagged.
  2. Unless otherwise specified, all angles are measured in radians, and all numbers used are real numbers.
  3. Unless otherwise specified, the domain of any function f is assumed to be the set of all real numbers x for which f ( x ) is a real number. The range of f is assumed to be the set of all real numbers f ( x ) where x is in the domain of f .
  4. In this test, ln x denotes the natural logarithm of x (that is, the logarithm to the base e).
  5. The inverse of a trigonometric function f may be indicated using the inverse function notation f-1 or with the prefix “arc” (e.g., sin-1 x = arcsin x)

5. Course Modules

Following are the main topics and percentages of the exam’s questions, mostly based on the College Board's description of the course:

Module 1: Limits  

  1.0 Introduction  

  1.1 Definition of a Limit   

  1.2 Computing Basic Limits   

  1.3 Continuity   

  1.4 Squeeze Theorem 

 

Module 2: Theory of the Derivative  

  2.0 Introduction

  2.1 Tangent Lines   

  2.2 Definition of Derivative   

  2.3 Rates of Change   

  2.4 Derivative Rules   

2.4.1 Fundamental Derivative Rules

2.4.2 Chain Rule

2.4.3 Derivatives of Exponential and Logarithmic Functions

2.4.4 Trigonometric Derivatives

2.4.5 Derivatives of Inverse Trigonometric Functions

  2.5 Higher Order Derivatives   

  2.6 Implicit Differentiation   

  2.7 L’Hôpital’s Rule   

  2.8 Some Classic Theoretical Results   

  2.9 Derivatives of Inverse Functions 

 

Module 3: Applications of the Derivative 

  3.0 Introduction

  3.1 Plotting with Derivatives   

3.1.1 Increasing and Decreasing Functions

3.1.2 Extrema

3.1.3 Concavity

  3.2 Rate of Change   

  3.3 Some Physics Problems  

 

Module 4: Theory of the Integral 

  4.0 Introduction

  4.1 Antidifferentiation   

  4.2 Definite Integral   

  4.3 Riemann Sums   

4.3.1 Riemman Sums Part I

4.3.2 Riemman Sums Part II

  4.4 The Fundamental Theorem of Calculus   

  4.5 Basic Integral Rules   

4.5.1 Basic Integral Rules I

4.5.2 Basic Integral Rules II

  4.6 U-Substitutions   

 

Module 5: Applications of the Integral  

  5.0 Introduction

  5.1 Area Under Curves   

5.1.1 Area Under Curves Part I

5.1.2 Area Under Curves Part II

  5.2 Average Value   

  5.3 Growth and Decay Models   

  5.4 Return to Physics   

 

6. About James Murphy

Dr. James Murphy is an applied mathematician. His research interests include harmonic analysis, machine learning, and the analysis of remote sensing data. Recent work has focused on fast algorithms for unsupervised learning and development of distance metrics for stochastic data models, with applications to hyperspectral imagery.

Dr. Murphy has taught at some of the world’s finest academic institutions, including the University of Chicago, the University of Maryland College Park, Duke University, and most recently at the Johns Hopkins University. His courses range from introductory statistics and precalculus to research topics courses for Ph.D. students. He was honored with the Aziz/Osborn Gold Medal in Teaching Excellence at the University of Maryland in 2013. He also works closely with undergraduates on research projects in both pure and applied mathematics. Several of his students are currently working on Ph.D.s at top universities. Dr. Murphy earned his Ph.D. in mathematics at the University of Maryland College Park in 2015. He earned his B.S. in mathematics from the University of Chicago in 2011, where he was a Student Marshal and Phi Beta Kappa.

 

7. How CLEP Works

Developed by the College Board, CLEP (College-Level Examination Program®) is the most widely accepted credit-by-examination program.

CLEP’s credits are accepted by 2,900 colleges and universities, according to the College Board. These tests assess college-level knowledge in 33 subject areas.

Modern States Education Alliance is the non-profit organization behind these edX-style courses. Its project is called “Freshman Year for Free” and its mission is to make college more accessible and affordable through free, high-quality online education.

• CLEP® Calculus: at a Glance

• 'Passing the CLEP and Learning with Modern States' orientation course